Solution Exercice 1 / Série 3

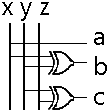
a) Table de vérité pour n= 3 bits

Dec Binaire Gray
  x y z a b c
0 0 0 0 0 0 0
1 0 0 1 0 0 1
2 0 1 0 0 1 1
3 0 1 1 0 1 0
4 1 0 0 1 1 0
5 1 0 1 1 1 1
6 1 1 0 1 0 1
7 1 1 1 1 0 0

Tableaux de Karnaught :

a :

  \z
xy\

 0 1
00 0 0
01 0 0
11 1 1
10 1 1
a = x
b :

  \z
xy\

 0 1
00 0 0
01 1 1
11 0 0
10 1 1
     _          _
b= x.y + x.y = x ⊕ y
c :

  \z
xy\

 0 1
00 0 1
01 1 0
11 1 0
10 0 1
     _          _
c= y.z + y. z = y ⊕z

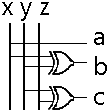b) Table de vérité pour n= 3 bits

Dec Gray Binaire
  a b c x y z
0 0 0 0 0 0 0
1 0 0 1 0 0 1
3 0 1 0 0 1 1
2 0 1 1 0 1 0
7 1 0 0 1 1 1
6 1 0 1 1 1 0
4 1 1 0 1 0 0
5 1 1 1 1 0 1

Tableaux de Karnaught :

x :

  \c
ab\

 0 1
00 0 0
01 0 0
11 1 1
10 1 1
x= a
y :

  \c
ab\

 0 1
00 0 0
01 1 1
11 0 0
10 1 1
     _          _
y= a.b + a.b = a ⊕b
z :

  \c
ab\

 0 1
00 0 1
01 1 0
11 0 1
10 1 0
z= a ⊕b ⊕c
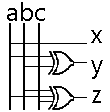